Compound Interest
Make Bank
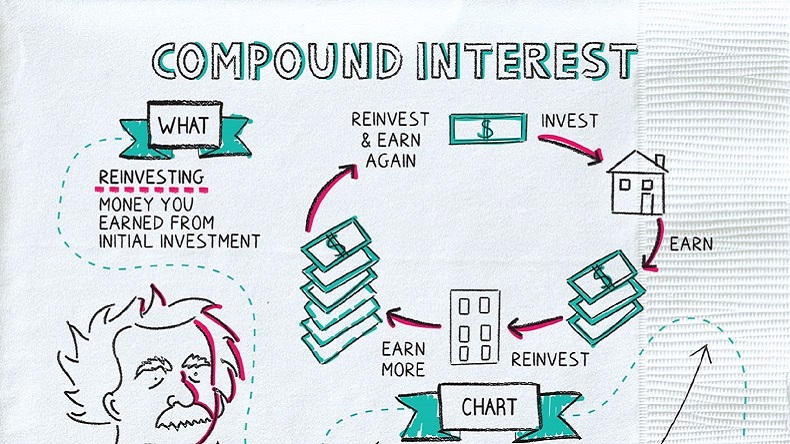

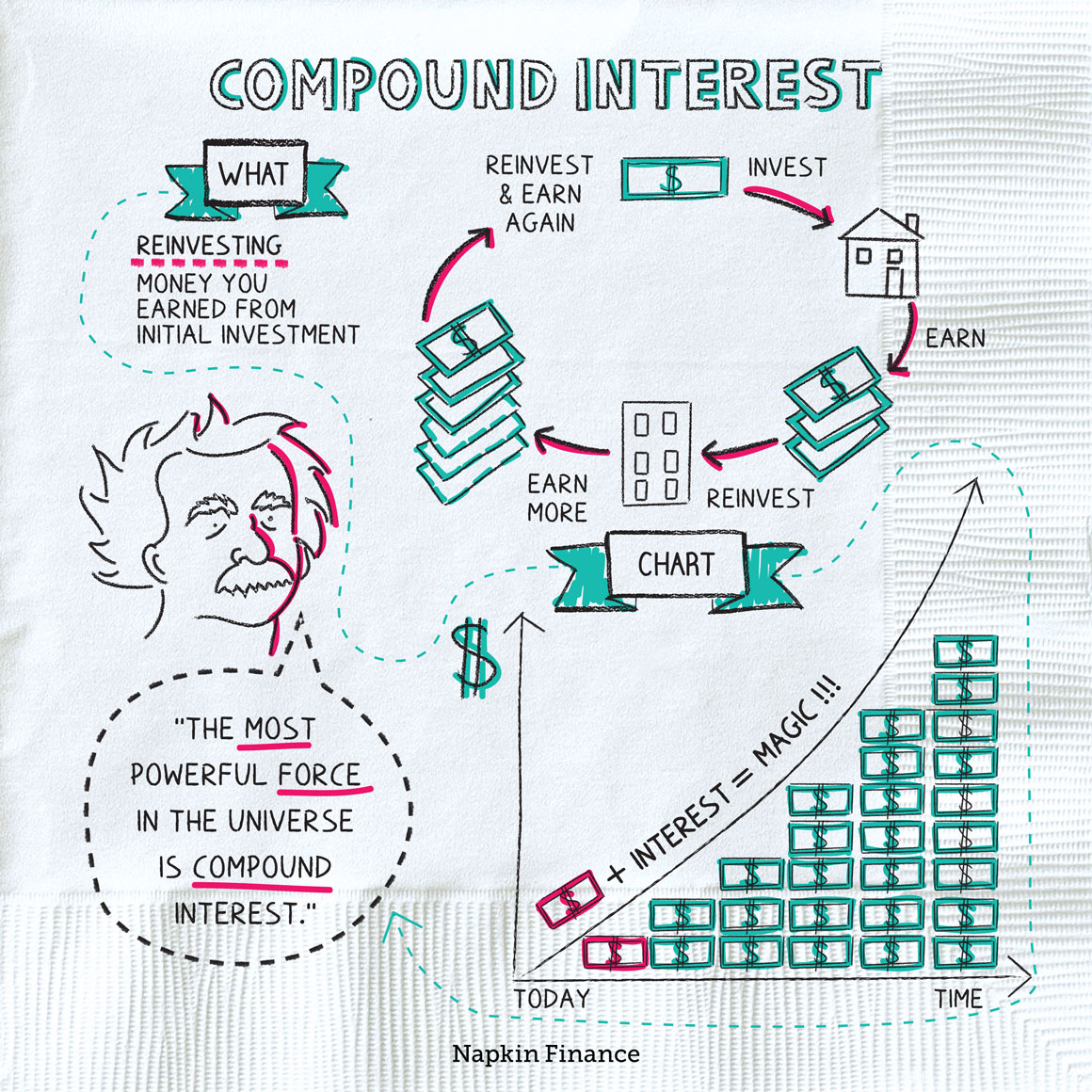
The most powerful force in the universe is compound interest.
— Albert Einstein
You’re probably already familiar with the basic concept of earning interest: You put $1,000 in the bank, and the bank pays you a little bit of interest in return, such as 2% per year. At the end of the year, you’ve earned $20.
Compound interest refers to earning interest on the interest you’ve already earned. If you keep holding your money in the bank, you’ll continue to earn interest not only on your original $1,000 but also on the $20 you earned. That means the amount of interest you earn will increase each year. In the second year, for example, you’ll earn $20 and 40 cents.
The magic of compounding is that your money grows at an increasing pace. That extra 40 cents may not sound like much. But over time and with big-enough numbers, compounding delivers mighty results.
Would you rather receive $10,000 a day, every day for a month or one penny that doubles each day for a month? (Hint: Yes, it’s a trick question!)
Thanks to the amazing math of compounding, at the end of one month, the doubling penny will have earned you $10,737,418 (and a massive need for some coin rollers) compared with $310,000 if you had collected $10,000 per day. Put another way, the doubling penny earns you 35 times what the $10,000-a-day option does.
Now do you believe in magic?
“My wealth has come from a combination of living in America, some lucky genes, and compound interest.“
—Warren Buffett
Let’s get real here. The reason the penny example delivers such big results is that it uses an absolutely massive interest rate. Doubling your money every day (meaning a 100% daily interest rate) is the same as an annual interest rate of about:
7,515,336,264,876,266,329,246,337,909,725,878,487,602,184,156,506,623,586,263,331,108,903,068,880,
366,747,019,083,836,794,831,259,849,702,191,923,100%
Any starting amount of money can grow into a giant pile of money with a big enough interest rate. Real-world numbers are typically a lot smaller.
Compounding always speeds along your money’s growth (unless you don’t let the interest you earn continue to grow). But three main things can help turbocharge your compounding:
- A higher interest rate
- A bigger starting sum of money or adding more money along the way
- More time to grow
Suppose you let your money grow for 10 years in the following situations:
| Starting sum of: | 2% rate | 10% rate |
| $1,000 | $1,219 | $2,594 |
| $100,000 | $121,899 | $259,374 |
Obviously, starting with more money is a big help. But the extra eight percentage points of interest makes an enormous difference too—at a 10% interest rate, you end the decade with twice as much money in each case as you would with a 2% rate. The extra interest helps your money compound faster.
Now suppose that instead of just 10 years you let your money grow for 30 years. And suppose that in each case you’re also able to save and invest an additional $5,000 every year:
| Starting sum of: | 2% | 10% |
| $1,000 | $204,652 | $839,919 |
| $100,000 | $383,977 | $2,567,410 |
With enough time, a solid interest rate, and the ability to add money to your stash, even the real-world numbers can get pretty big. Now that’s some magic you can actually use.
Savings accounts will compound your money. But because they pay low interest rates they do so very slowly. Billionaires like Warren Buffett put their money in investments that pay more over the long run, such as:
- Stocks
- Bonds
- Real estate
That’s because, as we saw above, even just a slightly higher rate can boost your money’s compounded growth by leaps and bounds.
Compound interest refers to earning interest on the interest you’ve already earned. Compounding has been called the eighth wonder of the world because of the amazing way it can grow small sums into vast riches. In the real world, you can boost the compounded growth of your money by saving more, letting your money grow for longer, and seeking higher rates by shopping around with different investments.
- How long will it take your money to double? Dividing the number 72 by your interest rate gives you a rough estimate. (It’s called the “rule of 72.”)
- The stock market’s long-term average return has been about 10%. Using the rule of 72, at that rate your money should double roughly every seven years.
- The average interest rate on a savings account is currently about 0.09%, but rates haven’t always been so meager. In the early 1980s, your money in the bank could earn almost 20% a year.
- Compounding interest is when you earn interest on interest. It’s what helps the wealthy turn money into more money.
- Investors talk about the “magic of compounding” because of the incredible way it grows your money at an ever-faster pace.
- Compounding can boost the growth of your savings account, but it’s also relevant to investments, which typically earn more.
- To enjoy the benefits of compounding, you have to reinvest and not spend what you earn.
- To increase your money’s compounded growth even more, try to invest more money, let your money grow for a longer period of time, and find the best return rate you can.